CS 210: Mathematical Logic Notes
Resolution 归结系统
是一种用于自动定理证明的逻辑推理规则
Normal form 范式
- 合取范式(Conjunctive Normal Form, CNF):为了应用归结推理,逻辑公式通常需要转换为合取范式,即多个子句的合取($\land$)。
- 析取范式(Disjunctive Normal Form, DNF):与之相应的,为多个子句的析取($\lor$)。

Literal 单式/文字

Clause子式/子句


任何Propositional language都可以表示成CNF和DNF
转换成CNF 和DNF 的方法

ps:2.的第三行的最后一个$\land$应该为$\lnot$
主合取/析取范式

主合取范式 (PCNF)
主合取范式是合取范式的一个特例,其中每个合取项(conjunct)都是一个或多个不同的原子公式的合取。换句话说,PCNF 中的每个子句都不包含重复的原子公式或其否定。
例如,逻辑表达式 (P ∨ Q) ∧ (P ∨ R)就是一个 PCNF,因为每个子句都是由不同的原子公式 P、Q 和 R 组成的合取。
主析取范式 (PDNF)
主析取范式是析取范式的一个特例,其中每个析取项(disjunct)都是一个或多个不同的原子公式的析取。这意味着 PDNF 中的每个子句都不包含重复的原子公式或其否定。
例如,逻辑表达式 (P ∧ Q) ∨ (P ∧ R) 就是一个 PDNF,因为每个子句都是由不同的原子公式 P、Q 和 R 组成的析取。
主范式的特点
- 无重复:在 PCNF 或 PDNF 中,每个子句都不包含重复的原子公式或其否定。
- 简化:主范式通常用于简化逻辑表达式,使逻辑推理和证明更容易进行。
- 转换:任何逻辑表达式都可以转换为等价的 PCNF 或 PDNF,尽管这种转换可能会增加表达式的复杂性。
Resolution归结/消解原理

Inference rules
- 通过归结原理合并:因为p和$\lnot$p矛盾,所以可以推出$\alpha\lor\beta$
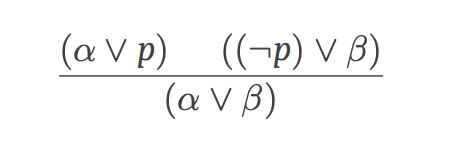
- Unit Resolution


The Resolution Proof Procedure

- 在Resolution系统中证明某命题,我们往往证明它的否命题可以推出矛盾
- 因为消解原理只能应用于析取子式,所以我们首先将表达式转化为合取范式
- 然后将CNF formulas 在$\land$ 处切分,得到clauses
- 反复应用消解原理,直到:
- 找到了空子句,即矛盾(参考Inference rules 第三点)即证明了原命题
- 无法再使用消解原理,那么我们得到结论无法推导出原命题
Example






